最近思い立って簡単なセル・オートマトンの計算をして、色々頭の体操をしている。
セル・オートマトン(英: cellular automaton、略称:CA)とは、格子状のセルと単純な規則による、離散的計算モデルである。計算可能性理論、数学、物理学、複雑適応系、数理生物学、微小構造モデリングなどの研究で利用される。非常に単純化されたモデルであるが、生命現象、結晶の成長、乱流といった複雑な自然現象を模した、驚くほどに豊かな結果を与えてくれる。
Wikipedia 「セル・オートマトン」より引用
30年くらい前に8ビット機のPC-8801で動作するライフゲーム(2次元セル・オートマトン)のプログラムを入力(作った訳ではない)して、変化するパターンを眺めていたのを思い出す。当時はPCの演算速度が遅く、マシン語のプログラムであったが、結構モタモタした動きであった。
良く考えると、Excelは、既にセルの表示機能が実装されているようなものなので、実はセル・オートマトンと相性が良さそうだと(今更ながら)気づき、VBAの練習がてら計算をしてみた。
1次元のセル・オートマトンについて、少しプログラムを作り、検討してみた。ひさびさのVBA なので勘が鈍っているが、なんとか完成。
今回検討した1次元セル・オートマトンは、標準的な2状態3近傍とした。すなわち、1つのセルには0か1の2つの状態のみが存在し、近傍に隣接する2つの状態によって定義されたルールに従って、次の時刻の自分のセルの状態が遷移する。
1つのルールにおける遷移条件は、対象の隣接(前後)のセルを含めた3ビット、すなわち(000)から(111)までの8通りの条件となる。従ってルールの種類の数は、2^8=256通りになる。このルールを8ビットの表現とし、0から255までの数値で表す(=ウルフラムコード)。
図1に、これらのルールのうち良く知られている「ルール184」の状態遷移図を示す。このルールは、交通流の渋滞モデルとして知られている。また、1次元の非線形波動を記述するBurgers方程式を「離散化」したものと等価であるという興味深い特徴を持つ。
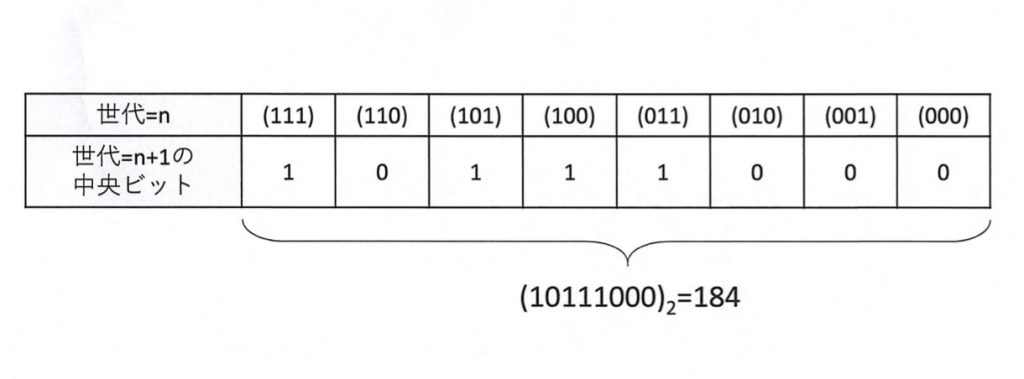
直観的には図2に示すように、セルの状態を、1=存在する、0=存在しないとして、自分のセルが「存在する」場合に
・前のセルにも「存在する」場合には、そこに留まる=移動できない
・前にセルに「存在しない」場合には、そこに進む=移動できる
という離散化された「流れ」を示していると理解できる。交通流における車の動きを単純化したものと言える。
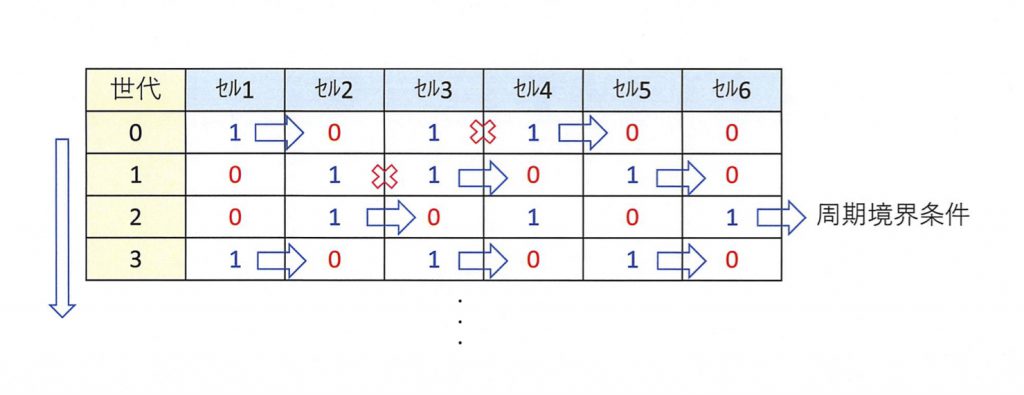
こうしたルールによって、初期の状態から時刻を順次変化させていった時に状態が最終的にどうなるかを、既にウルフラムら研究者が検討し様々な興味深い結果を得ている。単純に定常状態になるだけでなく、ランダムになったり、一定の周期を繰り返す状態など複雑な状態が生み出されることが明らかになっている。
ここでは、先人が既に解明したことの後追いであるが、少し計算した結果を示したい。宮崎市定の語る「無学者の二次方程式の解の公式の発見」の例となっている気もしないでもないが。
計算条件は、セル数を100とし、周期境界条件(左端と右端がつながっている)を設定した。
例えばルール184の時間発展は図3のようになる。初期密度を0.5としランダム配置した状態から開始している。初期段階の一部にあった密度の濃い部分(渋滞)が解消され、等間隔の定常状態になって収束していることがわかる。

ルール184は周期境界条件のもとで、1と0の数が保存する。また現在の状態から前の状態を一意に逆に生成できるため、可逆である。最終的には等間隔ピッチ(一つ起き)になる状態に近づくように安定する。
図4にルール30の時間発展の計算結果を示す。中央に1セルを設定することにより、カオス的な複雑なパターンとして増殖していく。

図5にルール110の時間発展の計算結果を示す。ルール30と同様に中央に1セルを設定すると、片側に複雑でありながらパターンを描きながら増殖していく。

図6にルール90の時間発展の計算結果を示す。中央に1セルを設定した場合には、良く知られているように自己相似なフラクタル図形を示す。
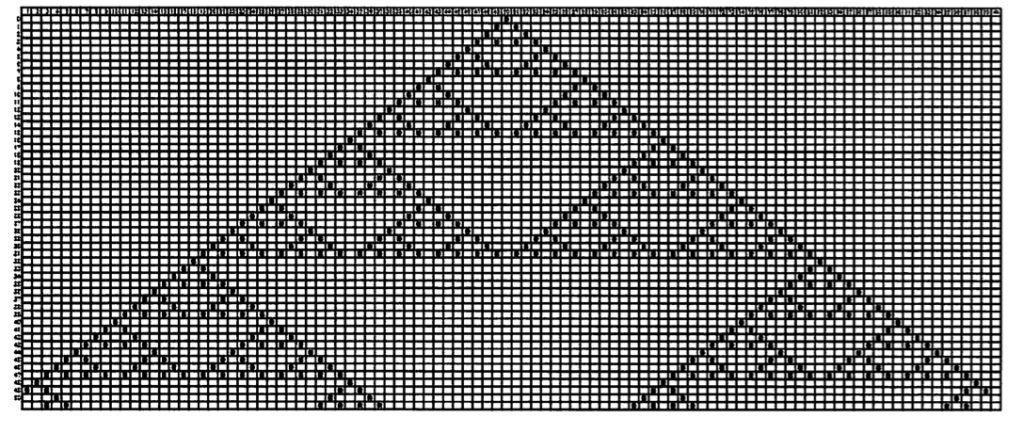
代表的なルールの時間発展を見てきたが、さらにルール自体をパラメータとして、このセルオートマトンの系の全体像を見てみたい。
各ルールの定常状態を示す因子として、十分に時間が経過した後のパターンのセルの状態を次の2つの変数で代表させることにする。
(1)密度:1の状態のセル数を全セル数で除したもの
(2)流量:流れとして例えた場合に、動くことができるセルの数を全セル数で除したもの
密度に関しては特に定義に問題ないが、流量についてはこの変数で表現することについては、疑問の余地がありそうだ。ルール184の交通流では流れのモデルになっているため、「流量」の表現は正しいが、他の場合には”10”というパターンの数、粗密を示した数値になっているだけである。
従って、ここではルール184の交通流における基本図である「密度-流量特性」の下で全ルールに対して計算結果を同一平面上にマッピングすることを目的とするに留めておきたい。
今回の計算では、収束させるための時刻(世代)計算数を1000とし(ただしカオス的な様相があることがわかっているので完全に収束はしない)、初期のセル配置を、密度を0から1までの範囲で30分割した上でランダムに配置することとした。
図7に0から255までのルールについて密度と流量の同一平面上にマッピングした結果を示す。ルール184の密度-流量の関係が示す、(密度,流量)=(0.5,0.5)の点を交点とした傾き45度と-45度の2直線が現れており、ピラミッド形状の下部の領域に全ての点がマッピングされている。
また時間発展の結果、1のセルが全て消失し0になってしまう場合もルールによってはかなりある。この場合は(密度,流量)=(0,0)の点に縮退することになる。
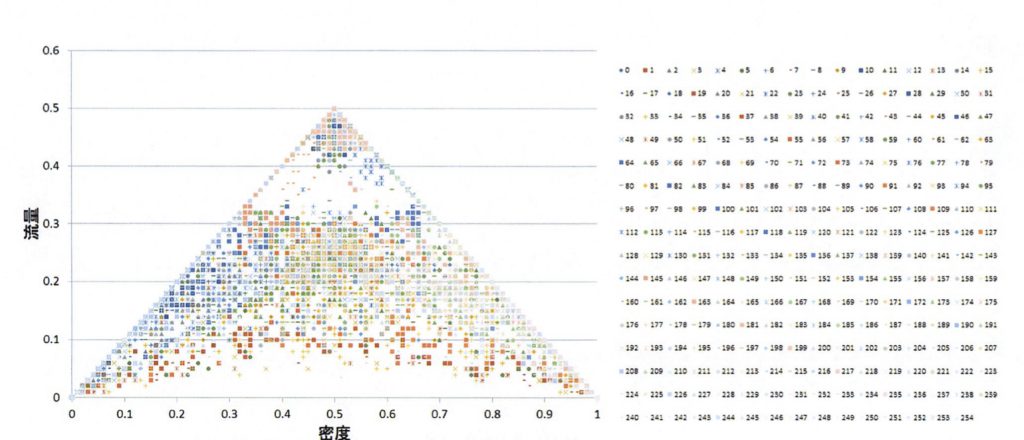
図7のグラフの色表現だと、ルール数での依存性、法則性が見えないので、図8に、ルール0から255に対してプロット点の色を赤(ルール0)から黄色(ルール255)に階調させて表現したものを示す。しかし、ここからも特にルールに依存する法則性は読み取れなかった。
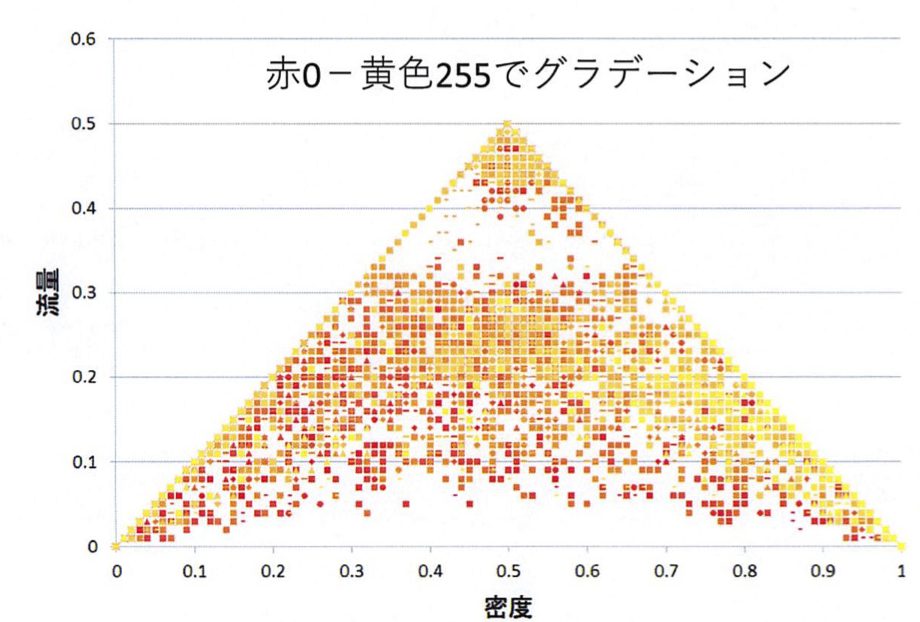
ちなみに、ルール184(10111000)のビット反転であるルール71(01000111)は全く異なる挙動を示す。一方ルール184は左から右に動く様相を示すが、右から左に動く場合のルールはルール226(11100010)となり、この場合には本質的に同じ結果になる。つまり、このルールのコードの記法に対称性がないので、階調表現では法則性が読み取れないのかもしれない。
この計算結果で疑問なのは、このプロットで埋められていない空白領域の存在である。空白領域はピラミッド形状の上方と底部に存在する。
この空白の領域は、どう解釈すれば良いのであろうか。
有名な「エデンの園配置」は、初期状態以外からはいかなる発展でも発生しない配置であるが、今回の計算では全ルールに対して「定常状態」に近い状態(ただし、カオス状態があるので定常状態にはならない)においても、密度-流量の2次元表現で空白領域が存在していることを示唆している。
また、全てが0になるパターンからも自明なように、ルールの中には不可逆、すなわち単射が存在しない系列があり、エデンの園配置が存在することは確かであろう。
定常状態において、いかなるルールでも最終的に存在しない状態の可能性があるとも言える(過渡的には存在している可能性はある)が、実際にはルール30のようなカオス的な発展を示すルールが存在するので、より初期値依存に対応した初期条件を精密にとった上で、十分長い時間を取ることにより埋まる部分と、エデンの園配置が混在した様相になっていると思われる。
このような単純な系であっても、そこから、”どうやっても辿りつけない領域が、すぐ近くにある”という、現実と薄皮一枚で異次元につながっているようなホラーSF要素を読み取るのは少し飛躍しすぎであろうか。
最後にやはり文中で言及した宮崎市定の語る「無学者の二次方程式の解の公式の発見」の例が自分で想起される結果になった。学問は、巨人の肩に乗らないと、なかなか苦しいのである。
(蛇足)VBAの計算で少しテクニカルな部分を、備忘的に記載しておく。
■ルール自体の数値化(変数化):セルオートマトンの「ルール」をブール型変数に格納しておく。具体的には1次元セルオートマトンのセル状態の状態遷移を、ブール型配列変数である「ルール(1)=(111)」から「ルール(8)=(000)」のそれぞれに対して、0の場合にはFalse、1の場合にはTrueというように定義すると良い。
■配列変数における周期境界条件の定義:剰余関数(MOD)を使用することで周期境界条件を考慮した配列パラメータが定義できる。例えば、10の剰余とはNを10で割った際の余りであり、Nを1から順番に増やしていった場合に、その回答が割る数10の周期0123456790123456789…と循環する。これを用いることで状態遷移判定の記述を一般化したまま周期条件条件を定義できた。